[백준] C++ 공유기 설치

우선 입력으로 20만까지 들어오고 공유기의 개수도 2 <=C <=N이기 때문에 모든 조합을 확인하는 것은 불가능하다.

어떻게 하면 시간복잡도를 줄일 수 있을까?

이 문제는 이분탐색을 활용하는 문제이다.

근데 이 문제는 특이하게 거리를 기준으로 이분탐색을 진행한다. 그래서 좀 헷갈렸던 거 같다.

거리를 기준으로 이분탐색을 한다는 말이 뭐냐면 만약 입력으로 1 2 4 8 9가 들어왔다고 치자.

그러면 가장 먼 거리는 (9-1)이고 가장 적은 거리는 (2-1)이다. 1과 8 이 거리 정보를 가지고 문제를 접근해야 한다.

 

두 집의 거리의 차이는 적어도 0보다는 크기 때문에 L을 1로 두고

두 집의 거리의 차이는 적어도 9보다는 작기 때문에 R을 8로 둔다.

L과 R의 합을 2로 나눈 값부터 확인해 나간다. (L+R)/2

(1+8)/2=4

먼저 거리 4부터 확인한다.

먼저 처음에 기준으로 잡는 것은 arr[0]이다. arr[0]부터 arr[N-1]까지 거리가 4 이상인 집을 찾으면 된다.

 

arr[0]과 arr[1]의 거리는 1이기 때문에 공유기를 설치하지 못하고 다음을 탐색한다. (기준으로 잡은 4보다 작음.)

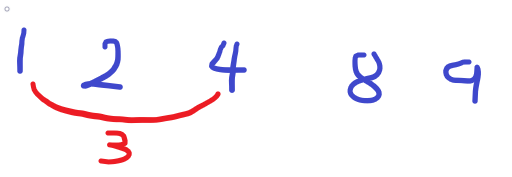
arr[0]과 arr[2]의 거리는 3이기 때문에 공유기를 설치하지 못하고 다음을 탐색한다. (기준으로 잡은 4보다 작음.)

arr[3]과 arr[0]의 거리가 7이기 때문에 arr[3]에 공유기를 설치한다.

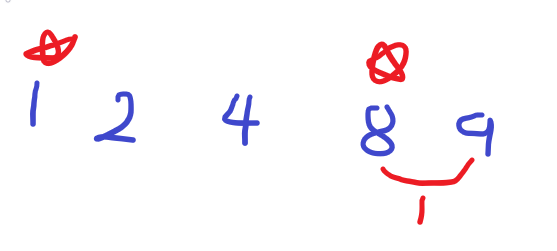
이제는 기준이 arr[3]이 되어 arr[3]과 arr[4]를 비교한다.

arr[4]와 arr[3]의 거리가 1이기 때문에 arr[4]에 공유기를 설치하지 못한다.

 

거리 4를 기준으로 잡고 탐색을 하였을 때 공유기를 2개 밖에 설치하지 못한다.

그래서 너무 기준을 크게 잡았기 때문에 R를 mid-1 해준다.

그러면 아까 L는 1이였고 이번에 새로운 R는 3(4-1) 이기 때문에 새로운 기준 거리는 (1+3)/2가 된다.

 

이런 느낌으로 계속해서 이분탐색을 진행하면 된다.

 

 

#include <iostream>
#include <algorithm>

using namespace std;

int arr[200001];

int main(void)
{
	int N = 0;
	int C = 0;

	cin >> N >> C;

	for (int i = 0; i < N; i++)
	{
		cin >> arr[i];
	}

	sort(arr, arr + N);

	int L = 1;
	int R = arr[N - 1] - arr[0];
	int result = 0;

	while(L<=R)
	{
		int mid = (L + R) / 2;
		int count = 1;

		int pre = arr[0];

		for (int i = 1; i < N; i++)
		{
			if (arr[i] -pre  >= mid)
			{
				pre = arr[i];
				count++;
			}
			
		}

		if (count >= C)
		{
			result = mid;
			L = mid + 1;
		}
		else
		{
			R = mid - 1;
		}
	}

	cout << result;


	return 0;
} // 1 2 4 8 9